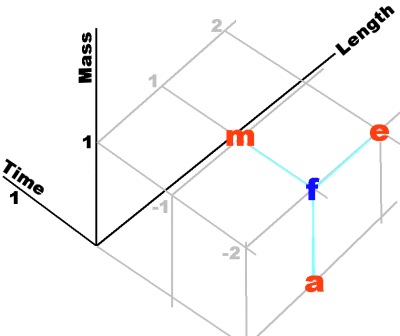
Idle musings on re-dimensioning dimensionsThere is no need to use QMLT (Charge-Mass-Length-Time) as fundamental dimensions - we could use other ‘units'. This note describes the process but offers no further insight save perhaps the observation that something can be put at the origin.Forgetting Charge for the momemt because I can't visualise in four dimensions, the standard Dimensions of physics are Mass, Length and Time. All other measurable quantities can be expressed in these dimensions; for example Density is mass divided by volume and volume is length cubed so the dimensions of density are [ML-3]. (Superscripts in HTML are a pain - I've just put the indices small) If we imagine a 3-space lattice with unit cubical graduations we can ‘place' Density one unit along the Mass axis and three units down (negative) the Length axis and no displacement from the Time axis. The figure shows (m)omentum (f)orce (e)nergy and (a)cceleration placed using this lattice.
Now ANY four non-planar points can be used to describe this 3-space. The illustration shows how we might very simply declare a new coordinate system on ‘m-e-a' relative to an origin of ‘f'. Any point describable by ‘MLT' can be described by ‘mea'. (I just chose ‘mea' by a 30 second inspection and for ease of presentation.) So for example in the mea system Mass is [M2 E-1 A0] and the MLT-origin is [M2 E-1 A-1] Actually the ‘mea' system should be the ‘meaf' system because we must specify the origin. In this case Force. Interestingly in this case Force is now dimensionless. I haven't a clue if this could be a handy thing to have when wrestling with physical equations. There are plenty of other possibilities and there is no requirement for the new set to be lined up with the existing lattice. How this works out when Charge is added I haven't the foggiest idea. Whether any of this is actually useful I can't say either.
|
©